Introduction to Space Physics Learning Notes

2. PHYSICS OF SPACE PLASMAS

2.1 INTRODUCTION

1. Plasmas in space atr extremely tenuous gases of ionized particles.
   • on average, there is no net charge
2. the density is too low \(\rightarrow\) the encouters between particles can be ignored
   • we need only consider the responses of the charged particles to the force fields

2.2 SINGLE-PARTICLE MOTION

1. Maxwell's Equations are as follows. In Space Physics, \(\mathbf{D}=\epsilon_0\mathbf{E},\mathbf{H}=\frac{\mathbf{B}}{\mu_0}\) (SI Units), \(\mathbf{D}=\mathbf{E},\mathbf{H}=\mathbf{B}\) (Gaussian Units)
   • 
2. \(\mathbf{B}=\nabla \times \mathbf{A}\ ;\ \mathbf{E}=-\nabla\phi-\frac{\partial \mathbf{A}}{\partial t}\)
   • \(\phi\) : scalar potential
   • \(\mathbf{A}\) : vector potential
3. \(m\frac{d\mathbf{v}}{dt}=q\mathbf{E}+q\mathbf{v}\times\mathbf{B}+\mathbf{F_g}\), \(\mathbf{F_g}\) is nonelectromagnetic forces (such as gravitational forces)
   • \(\mathbf{F_g}=0,\mathbf{E}=0,\mathbf{B}=B\vec{e_z}\) :
     • \(m\dot{v_x}=qv_y B\ ;\ m\dot{v_y}=qv_x B\)
     • \(\ddot{v_j}=-(\frac{qB}{m})^2v_j=-\Omega_c^2v_j\ \ \ \ (j=x,y\ ; \ \Omega_c=\frac{qB}{m})\)
     • cyclotron/Larmor radius : \(\rho_c=\frac{v_{\perp}}{\Omega_c}=\frac{m v_{\perp}}{qB}\)
     • circular motion in the uniform magnetic field does not change particle's kinetic energy : \(m\frac{d\mathbf v}{dt}\cdot \mathbf{v}=\frac{d(\frac 1 2 mv^2)}{dt}=q\mathbf{v}\cdot (\mathbf{v\times B})=0\)
   • \(\mathbf{F_g}=0,\mathbf{E}\neq0,\mathbf{E\cdot B}=0,\mathbf{B}=B\vec{e_z}\) :
     • 
     • the particle drift velocity : \(\mathbf{u_E}=\frac{\mathbf{E\times B}}{B^2}\)
     • for arbitrary forces : \(\mathbf{u_F}=\frac{\mathbf{F\times B}}{qB^2}\)
   • a gradient in the field strength in the direction perpendicular to \(\mathbf{B}\) :
     • \(\mathbf{u_g}=\frac{1}{2}mv_{\perp}^2\mathbf{B\times}\frac{\nabla \mathbf{B}}{qB^3}\)

4. THE SOLAR WIND

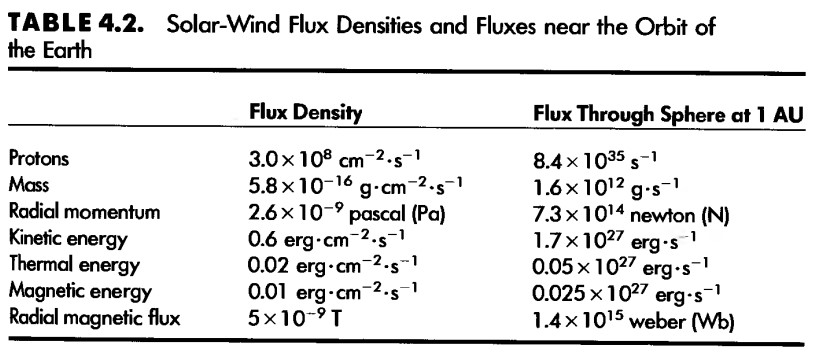
4.1 A QUICK SURVEY OF SOLAR-WIND PROPERTIES

1. THREE LISTS
   • 
   • 
   • 
2. the solar wind that blows past the earth is hot, tenuous and fast-moving by terrestrial standards
   • it consists largely of ionized hydrogen, with a small admixture of ionized helium(5%) and fewer ions of heavier elements
3. the pressure in an ionized gas with equal proton and electron density \(n\) :
   • \(p_{gas}=nk(T_p+T_e)\)
     • \(T_p,T_e\) are the proton and electron temperatures
     • \(p_{gas}=30\ pico\ pascals(pPa)\)
4. sound waves in an ionized gas with pressure \(p_{gas}\) and mass density \(\rho=n(m_p+m_e)\) travels at a speed :
   • \(c_s=\{\frac{\gamma p}{\rho}\}^{\frac{1}{2}}=\{\frac{\gamma k}{m_p+m_e}(T_p+T_e)\}^{\frac{1}{2}}\)
     • \(\gamma=\frac{C_p}{C_v}\), for hydrogen : \(\gamma=\frac{5}{3}\)
     • \(c_s\approx60\ km\cdot s^{-1}\)
     • solar-wind flow is highly supersonic (\(400\ km\cdot s^{-1}\))
5. the magnetic field can be thought of as exerting a pressure :
   • \(p_{mag}=\frac{B^2}{2\mu_0}\approx 15\ pPa\)
   • comparable to the gas pressure
   • indicate that magnetic effects will be about as important as pressure effects in the solar-wind plasma

7. IONOSPHERES

7.1 THE UNDERLYING ATMOSPHERE

1. The density \(n_n\) of a constituent of the upper atmosphere obeys hydrostatic equation:
   • \(n_n m_n g=\frac{dp}{dh}=-\frac{d}{dh}(n_n kT_n)\)
     • shows a balance between the vertical gravitational force and the thermal-pressure-gradient force
     • \(m_n\) : molecular or atomic mass
     • \(h\) : altitude
     • \(p=n_nkT_n\) : thermal pressure
2. assume that \(T_n\) is independent of \(h\) :
   • \(n_n=n_0\exp\frac{-(h-h_0)}{H_n}\)
     • \(H_n=\frac{kT_n}{m_n g}\) : the scale height of the gas
     • \(n_0\) : the density at the reference altitude \(h_0\)
     • the lightest molecules and atoms have the largest scale heights
     • \(T_n\) may depend on \(h\) the equation is not enough

7.2 ION PRODUCTION

7.2.1 Photoionization

simplifying assumption \(\rightarrow\) Chapman Theory

9. THE MAGNETOPAUSE, MAGNETOTAIL, AND MAGNETIC RECONNECTION

9.1 THE MAGNETOPAUSE

1. the magnetopause : the upper boundary of the atmosphere
2. It separates the geomagnetic field and plasma of terrestrial origin from solar-wind plasma.